 Figure 1 - Typical butterfly style DFG. |
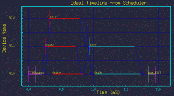 Figure 2 - Resulting time-line graph. |
A parallel corner-turn requires a slice of data from every processor in one stage to be transfered to every processor in the next stage. The problem is further complicated by the fact that the number of processors in each stage may be different. Lets call these parameters Nstg1 and Nstg2. We need to be concerned that the proper quantity of data is transferred and shows-up on each processor, and that the proper amounts kick-off the correct process tasks mapped the to right processors.
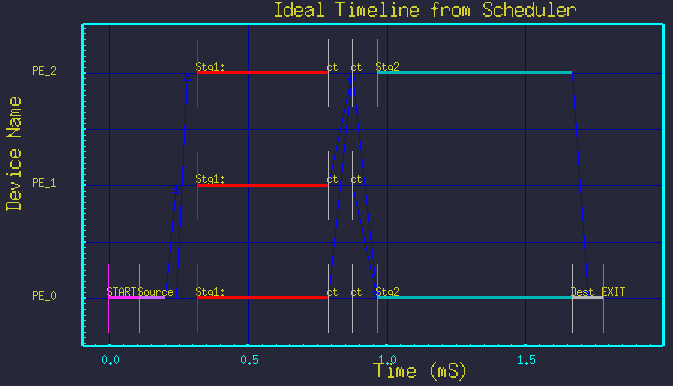
Consider the typical butterfly style DFG in figure 1. It shows processing of the first stage split into 3 parallel branches, with the second stage split into 2 parallel branches. Figure 2 shows the resulting time-line graph.
 Figure 1 - Typical butterfly style DFG. |
 Figure 2 - Resulting time-line graph. |
A method to express the parallelization parametrically is shown in figure 3. The data amounts on the arcs become expressions of the parameters, which imply arbitrary parallelization or gathering for the following stages. Figure 4 shows the resulting time-line for the above parameters.
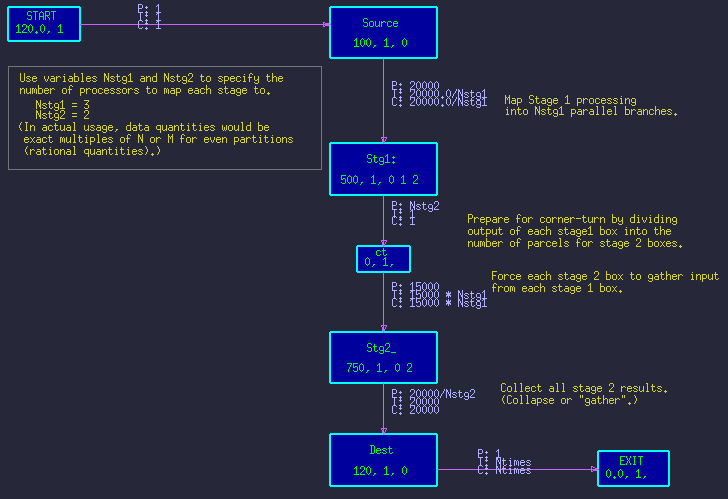
Note: The compute-time values are often parametric accordingly, but this is not the concern of this discussion. Likewise, the base data quantities are usually parameters two, but again we did not wish to add unnecessary complexity.
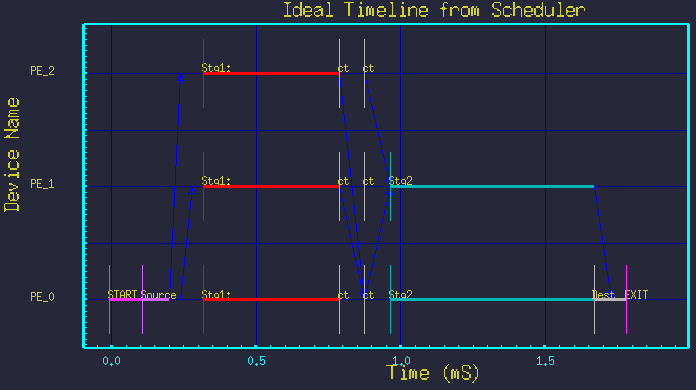
Next we show that by merely changing the two parameter values, we see new mappings without modifying the graph structure at all. Figures 5 though 9 show the mappings resulting from different parameter settings.
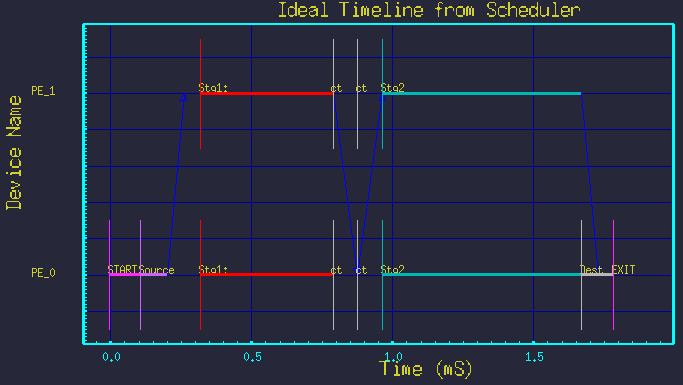
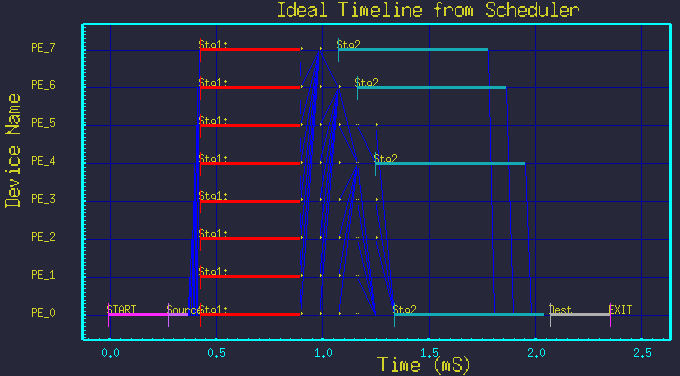
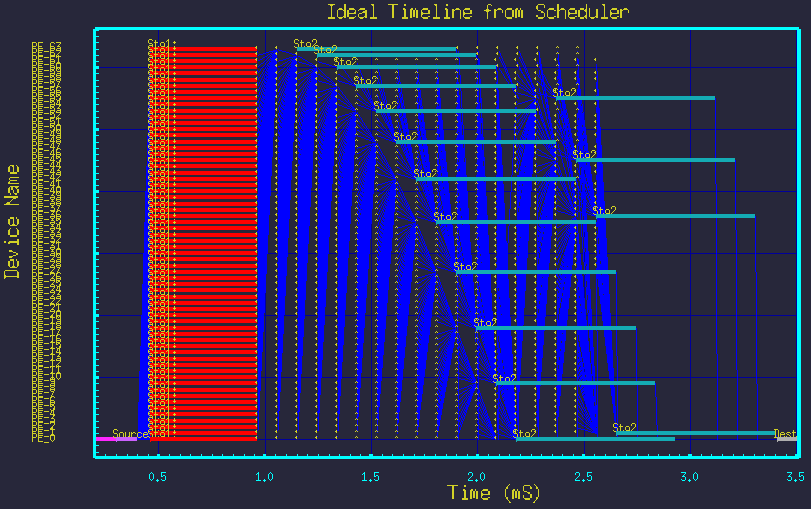
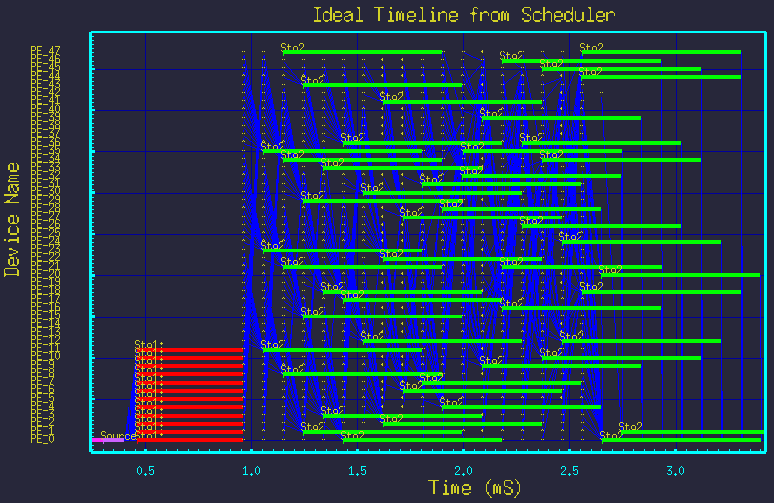
... And of course, we must show it still works for the trivial case:
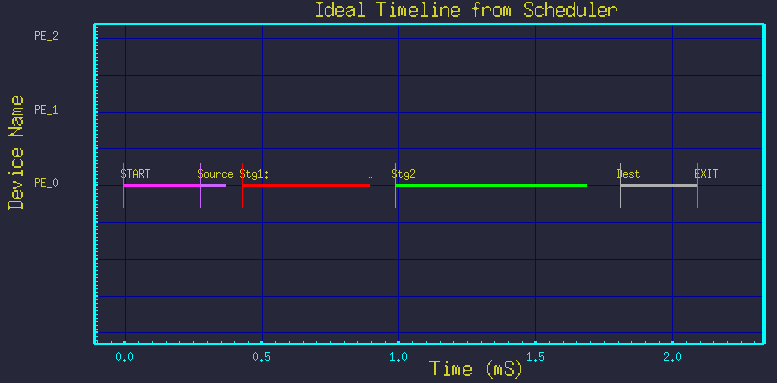
All the above timelines were made from the same DFG in figure 3, but merely by changing the parameters Nstg1 and Nstg2. The structure of the graph was not changed.
One additional note is that the node, ct, is essentially an artificial node for distributing the data in the proper ratios. Normally, it's compute-time is set to zero (0.0), so it has no effect on the graph, other than data-distribution. Consequently, the arc from Stg1 to ct is essentially artificial as well, and to avoid the potential impact and clutter of the minimum 1-byte transfers, the arc's NoXfer attribute is set to true.
For example, some of the cases run above did not use any explicit mappings. (The mapping field of all nodes was blank, so the Scheduler selected processors for us.) We can force the tasks to run on specifc processors by naming the processors explicitly in the mapping field of the first and second stage nodes. Figure 10 shows the timeline resulting from the DFG of Figure 3, but with the mapping of node, Stg2, set to: 0 2 (as in /PE_0 /PE_2). Note: The mapping field is a space delimited list.
The mapping/assignment list of the CSIM Scheduler is often under-estimated. There are many things that can be done with it.
Some things everyone should know about mapping assignments: