Parametric DFG Mapping

Many first time DFG users hard-wire their diagrams to specific mapping structures. If the mapping changes, the graph needs to be edited. For example, suppose a stage of processing is drawn as ten parallel DFG branches to show, -and to force-, a parallelization of ten. Now if the parallelization needs to be increased or decreased, the graph must be edited to add or remove branches of processing. This involves connecting and parameterizing new boxes and arcs, or cutting them away. Clearly an awkward process, if this changes often.

Sometimes a better way is to specify parallel mappings parametrically instead of graphically. The parallelization can then be controlled by concise expressions. (However the explicitness in the graphical view is diminished as well.)

As an example, we'll consider the corner-turn or butterfly operation, also known as matrix transpose for data-domain decomposition mappings. The corner-turn is a good example because it exhibits complex data interactions, and occurs quite commonly in many applications. It is also very regular and lends itself well to parametric description.

A parallel corner-turn requires a slice of data from every processor in one stage to be transferred to every processor in the next stage. The problem is further complicated by the fact that the number of processors in each stage may be different. Lets call these parameters Nstg1 and Nstg2. We need to be concerned that the proper quantity of data is transferred and shows-up on each processor, and that the proper amounts kick-off the correct process tasks mapped the to right processors. -- Clearly a daunting problem if solved manually for large graphs. Fortunately, CSIM's Scheduler provides convenient methods for automating such mappings.

Consider the typical butterfly style DFG in figure 1. It shows processing of the first stage split into 3 parallel branches, with the second stage split into 2 parallel branches. Figure 2 shows the resulting time-line graph.

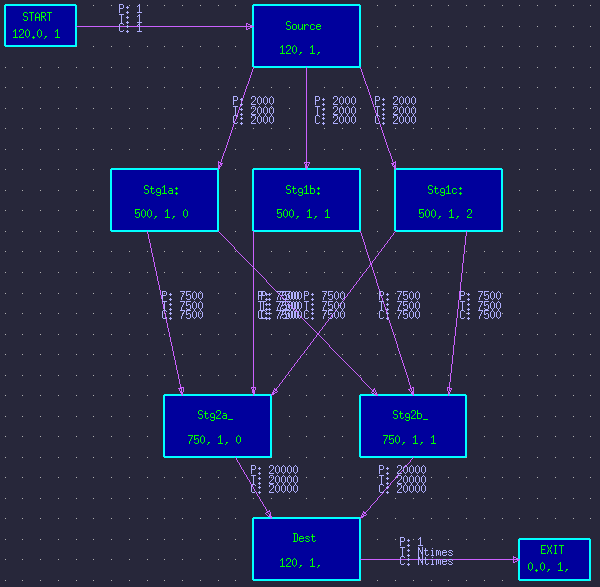
Figure 1 - Typical butterfly style DFG.

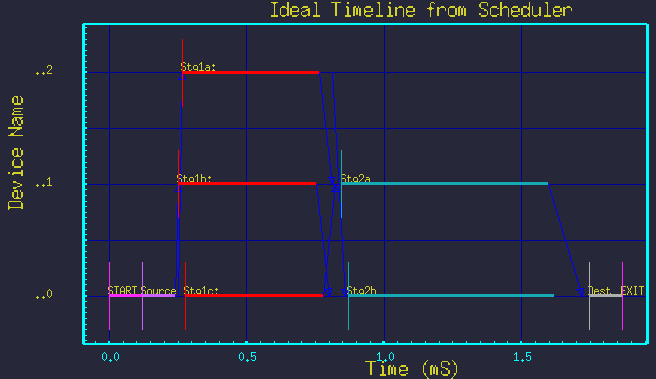
Figure 2 - Resulting time-line graph.

However, if we later learn that the preliminary allocations exceeded processor capabilities, it would be tedious to redraw the graph, for example with four nodes in stage one, and three in stage two.

A better approach is to use parameter-based mapping. Two such methods are described below. The first method is traditional, but has some limitations. But the discussion is retained as a link, because it is a good example of how to do more general things with only the basic flow-graph rules. The second method is newer and easier to use, and it's discussion is included in full text below..

Parametric Mapping Method I

(This earlier method is now depreciated in favor of Method-II below.)

Parametric Mapping Method II

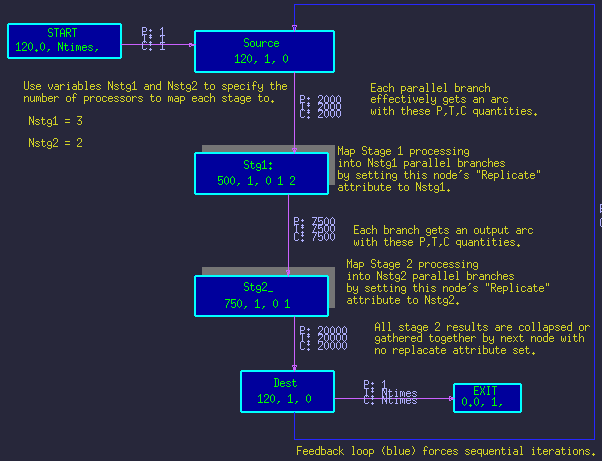
Figure 3 - Parametric DFG.

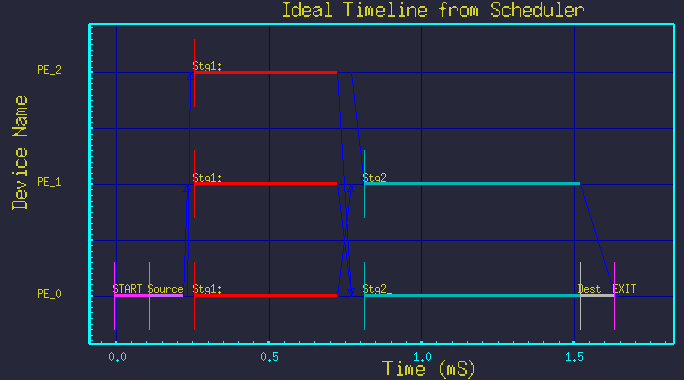
Figure 4 - Resulting time-line graph for parametric mapping.
(Nstg1=3, Nstg2=2)

Note: The compute-time values are often parametric accordingly, but this is not the concern of this discussion. Likewise, the base data quantities are usually parameters too, but again we did not wish to add unnecessary complexity.

You may download the DFG in figure 3 by clicking here. You can practice scheduling it without need of a hardware architecture, by specifying a number of processors on the command-line and by not specifying the netinfo file. Example, the timeline above was created with:

sched -n 10 Mapping.dfg

xgraph IdealSpiderweb.dat IdealTline.dat &

Next we show that by merely changing the two parameter values, we see new mappings without modifying the graph structure at all. Figures 5 though 7 show the mappings resulting from different parameter settings.

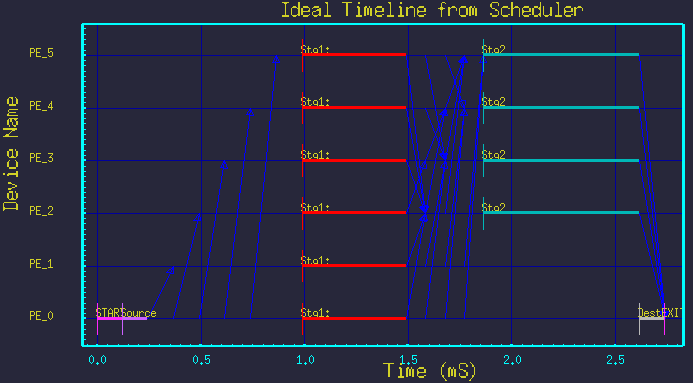
Figure 5 - Time-line for Nstg1=6, Nstg2=4.

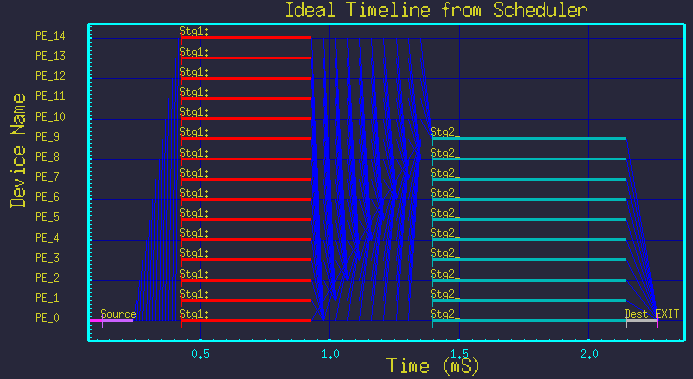
Figure 6 - Time-line for Nstg1=15, Nstg2=10.

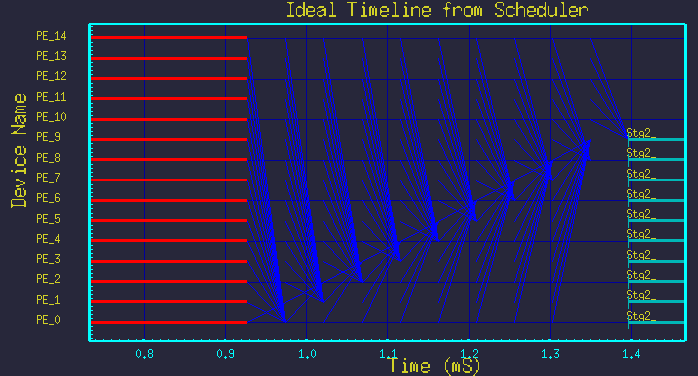
Figure 7 - Blow-up of the transfers above.

All the above timelines were made from the same DFG in figure 3, but merely by changing the parameters Nstg1 and Nstg2. The structure of the graph was not changed.

This method is different from the method-1 in that it does not require using an intermediate CT node, nor explicitly multiplying the produce amounts.

Mapping Control

For example, some of the cases run above did not use any explicit mappings. (The mapping field of all nodes was blank, so the Scheduler selected processors for us.) We can force the tasks to run on specific processors by naming the processors explicitly in the mapping field of the first and second stage nodes. Figure 8 shows the timeline resulting from the DFG of Figure 3, but with the mapping of node, Stg2, set to: 3 4 1 2 (as in /PE_3 /PE_4 /PE_1 /PE_2). Note: The mapping field is a space delimited list.

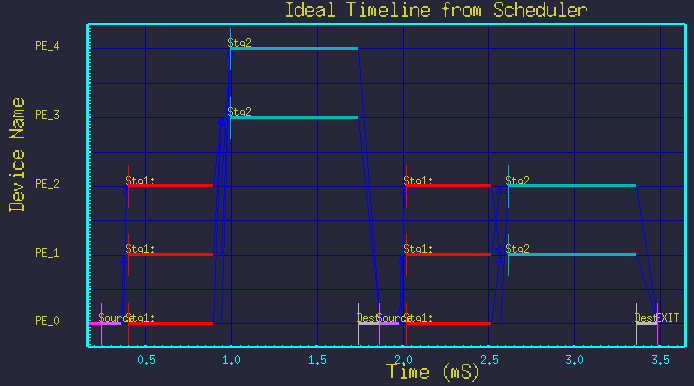
Figure 8 Time-line for explicit mapping.

Some things everyone should know about mapping assignments:

1. You can specify parallel assignments. For example, suppose you want a specific task to be mapped in parallel to three computers. Simply name them in the list: PE1 PE2 P3

2. You can specify sequences of parallel mappings. Suppose you want a specific task to be mapped in parallel first to three computers, next to three others, and then back again to the first three, and so on. Simply name them in the list: PE1 PE2 P3   PE4 PE5 PE6   PE7 PE8 PE9. The list will repeat in a round-robin fashion, each time the sequence is exhausted.

3. You can specify First-Available-From-a-Group mappings. That is, you can designate a group of processors that a set of tasks will map to. But not any specific order. To do this, set the task node type to be GetAny, then list the processors.

4. You can specify groups of processors as macros. This is especially handy when mapping large sections of DFG's (many nodes) to various groups. This way, you need only change one definition to alter the mapping of many tasks.

5. Task groupings can be hierarchical. This provides very rapid remapping of your DFG's. For example, you can define subgroup1 = PE1 PE2, and subgroup2 = PE3 PE4, through subgroup40, etc.. If you define GroupA to be the subgroups from 1-9, and GroupB to be the subgroups from 10-19, then you can conveniently map a highly parallel task to many processors by simply mapping it to GroupA GroupB. Etc..

Addendum -

.